기본 개념
신호 대 잡음비(Signal-to-Noise Ratio, SNR)는 통신 신호의 품질을 나타내는 핵심 지표로, 신호 세기와 잡음 세기의 비율을 의미합니다. 값이 높을수록 신호가 더 명확하고 잡음의 영향이 적어 통신 신뢰성이 향상됩니다. 반대로 값이 낮으면 신호가 잡음에 묻혀 데이터 오류나 손실이 발생하고 성능 저하로 이어질 수 있습니다. 이번 글에서는 SNR의 계산 방법과 그 의미, 활용 사례를 살펴보겠습니다.
SNR 계산 방법 (Signal-to-Noise Ratio)
SNR은 '신호 전력과 노이즈 전력의 비'로 정의됩니다. 일반적으로 다음과 같은 공식으로 표현합니다
- 비율 공식: SNR = P_signal / P_noise (신호 전력 P_signal을 노이즈 전력 P_noise로 나눈 값)
- 데시벨(dB) 단위: SNR_dB = 10 · log10(P_signal / P_noise) (로그 스케일로 표현)
- 만약 신호와 노이즈를 **전압(V)**으로 측정했다면 전력이 전압의 제곱에 비례하므로 20 · log10(V_signal / V_noise) 형태로 계산합니다.
예를 들어, 신호 전력이 -60 dBm이고 노이즈 전력이 -90 dBm이라면, 두 값의 차이인 30 dB가 SNR이 됩니다. (계산: SNR_dB = -60 dBm - (-90 dBm) = 30 dB)
SNR의 의미와 중요성
SNR 값은 1(또는 0 dB)을 기준으로 신호가 노이즈보다 강한지 또는 약한지를 판단할 수 있습니다
아래에서는 SNR이 낮을 때와 높을 때 각각 어떤 의미를 갖는지 정리합니다:
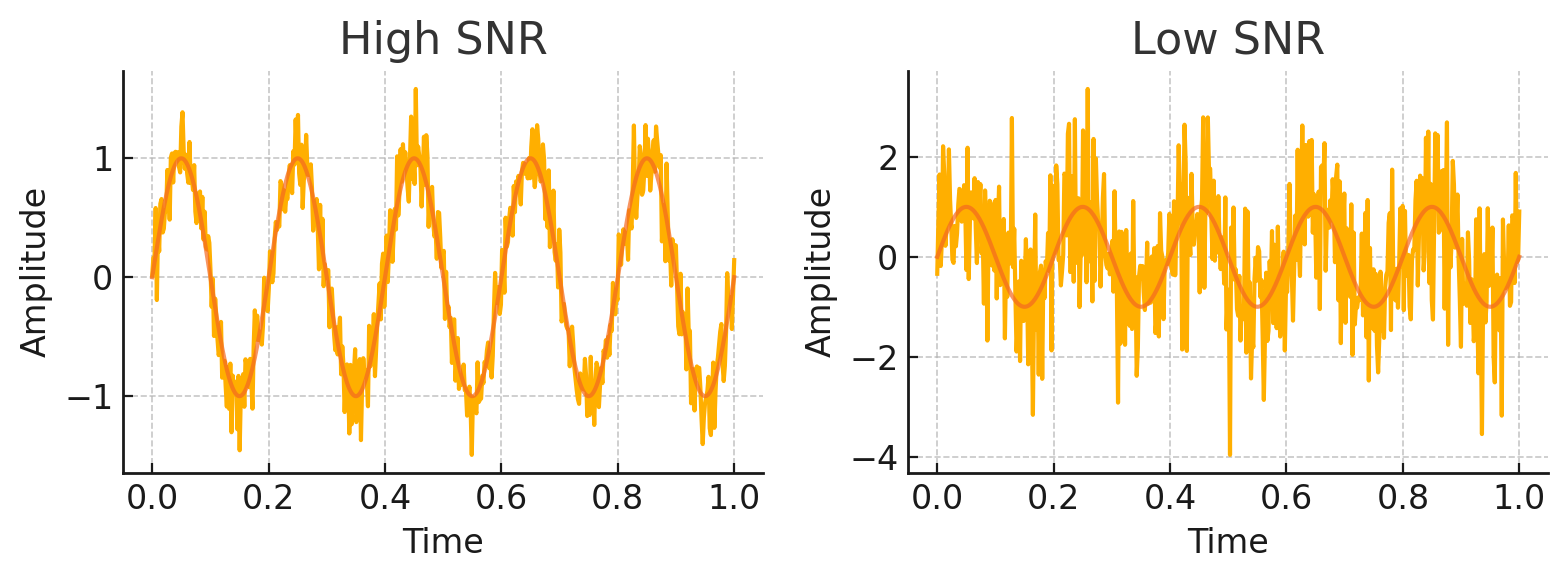
- SNR < 1 (SNR_dB < 0 dB): 신호 전력이 노이즈 전력보다 작은 상황을 의미합니다. 이 경우 신호가 잡음에 파묻혀 통신이 어려워지거나 불가능할 수 있습니다. 해결을 위해 신호 세기를 높이거나 노이즈를 줄여 SNR을 개선해야 합니다.
- SNR > 1 (SNR_dB > 0 dB): 신호 전력이 노이즈 전력보다 큰 상황을 의미합니다. 일반적으로 SNR이 높을수록 신호가 더 명확하여 수신기에서 신호 검출이 수월하고 데이터 전달이 신뢰성 있게 이루어집니다. 그러나 SNR이 높다고 해도 그 값이 충분히 크지 않으면, 원하는 신호와 잡음을 구분하기 어려워 데이터 오류가 발생할 수 있습니다. 실제로 SNR이 낮은 경우 데이터 패킷이 손실되어 재전송이 발생하고, 그로 인해 처리량(throughput)이 감소하고 지연(latency)이 증가하는 현상이 나타납니다
SNR의 활용 사례
SNR은 다양한 분야에서 신호 품질을 평가하고 시스템을 최적화하는 데 활용됩니다
주요 활용 사례
- 무선 통신 (Wi-Fi, 5G, LTE 등): 무선 환경에서 수신 신호 세기와 잡음 수준을 비교하여 신호 품질을 분석하고 최적의 안테나 배치나 전송 전력을 조절하는 등 네트워크 성능 최적화에 활용합니다. 높은 SNR은 더 넓은 커버리지와 안정적인 연결을 의미합니다.
- 오디오 및 영상 전송: 마이크, 카메라, 방송 장비 등에서 신호 왜곡과 잡음을 최소화하기 위한 지표로 사용됩니다. 예를 들어, 오디오 녹음에서 SNR이 높으면 잡음이 적고 음질이 선명하며, 영상에서도 SNR이 높을수록 화질 저하 없이 깨끗한 화면을 얻을 수 있습니다.
- Shannon–Hartley 이론: 정보이론에서 채널 용량 C (최대 데이터 전송 속도)는 대역폭 B와 SNR에 의해 결정되는데, 공식으로 C = B · log2(1 + SNR)로 표현됩니다. 즉 주어진 대역폭에서 SNR이 높을수록 전송할 수 있는 데이터 양이 증가합니다. 이 관계를 통해 통신 시스템에서 필요한 SNR 수준을 계산하고 시스템 설계에 활용합니다.
결론
신호 대 잡음비(SNR)는 신호의 품질과 명료도를 좌우하는 중요한 지표입니다. SNR이 높을수록 신호가 잡음보다 충분히 강해 데이터 전송이 안정적이며, SNR이 낮으면 신호가 흐려져 성능 저하나 통신 장애가 발생할 수 있습니다. 이러한 이유로 SNR은 통신, 오디오, 영상 등 다양한 분야에서 신호 품질 평가와 개선을 위해 적극 활용되며, 엔지니어는 SNR을 관리함으로써 신뢰성 높은 시스템을 구현할 수 있습니다.
'AI > (PJT)음성 화자 분류' 카테고리의 다른 글
| COPS-KMeans (Constrained Over-Partitioning Spectral K-Means) (0) | 2025.03.20 |
|---|---|
| MFCC (Mel-Frequency Cepstral Coefficients) (1) | 2025.03.20 |
| 음성 화자 분류 시작하기 (0) | 2025.02.28 |